Вероятность поражения цели

117. При стрельбе из стрелкового оружия по одиночным живым целям и из гранатометов по одиночным бронированным целям одно попадание обычно дает поражение цели. Поэтому под вероятностью поражения одиночной цели понимается вероятность получения хотя бы одного попадания при заданном числе выстрелов.

118. Вероятность поражения цели при одном выстреле (Pi) численно равна вероятности попадания в цель (р). Расчет вероятности поражения цели при этом условии сводится к определению вероятности попадания в цель.

Пример. Определить вероятность поражения снайпера противника (грудная фигура) с первого выстрела из снайперской винтовки обр, 1891/30 г. на расстояние 500 м; расстояние до цели определено глазомерно.

Решение. 1. По таблицам находим: Bв = 0,08 м; В6 = 0,08 м; из приложения 4 (табл. 7 в 6) ошибка в подготовке стрельбы по высоте

Ев = 0,36 м, приведенные размеры цели: высота 0,45 м, ширина 0,45 м.

2. Определяем суммарную (приведенную) ошибку в подготовке стрельбы по высоте:

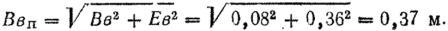
3. Определяем вероятность попадания в цель:

а) в полосу, равную приведенной высоте цели:

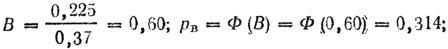
б) в полосу, равную приведенной ширине цели:

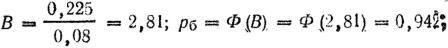
в) в цель:

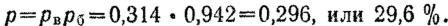
Так как при попадании пули в снайпера будет наверняка получено его поражение, найденное значение вероятности попадания и есть вероятность поражения цели с первого выстрела, т е. р = Pi = 29,6%.

119. Вероятность поражения цели (Pi) при нескольких одиночных выстрелах, одной очередью или несколькими очередями, когда вероятность попадания для всех выстрелов одинакова, равна единице минус вероятность промаха в степени, равной количеству выстрелов (n), т. е.

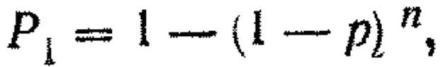
Пример. Определить вероятность поражения реактивного противотанкового ружья при стрельбе из пулемета Калашникова одной очередью в 5 выстрелов на расстояние 600 м; ветер боковой; расстояние до цели определено глазомерно.

Решение. 1, По таблицам находим: Bв Сум = 0,44 м, Вб сум = 0,61 м; из приложения 4 (табл. 7 и 6) срединная ошибка по высоте .Ев = 0,63 м, по боковому направлению Ен = 0,43 м, коэффициент фигурности 0,72.

2. Определяем суммарную (приведенную) ошибку в подготовке стрельбы по высоте:

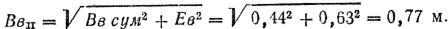
3. Определяем суммарную (приведенную) ошибку в подготовке стрельбы по боковому направлению:

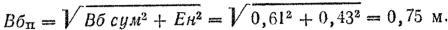
4. Определяем вероятность попадания в цель:

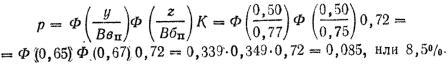
5. Определяем вероятность поражения цели очередью в 5 выстрелов:

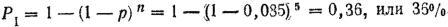
Найденная таким образом вероятность поражения цели характеризует надежность стрельбы, т. е. показывает, в скольких случаях нз ста в среднем цель в данных условиях будет поражена не менее чем при одном попадании. По условиям примера при большом числе подобных стрельб в среднем на каждые 100 стрельб в 36 стрельбах будет получено не менее одного попадания в цель, в 64 стрельбах цель не будет поражена.

Стрельба считается достаточно надежной, если вероятность поражения цели не менее 80%.

120. Вероятность поражения цели при нескольких выстрелах одной очередью или несколькими очередями, когда вероятность попадания первых и последующих пуль (очередей) изменяется от выстрела (очереди) к выстрелу (очереди), равна единице минус вероятность промахов первых и последующих пуль очереди (очередей):

а) для одной очереди:

б) для нескольких очередей (вероятность попадания от очереди к очереди не изменяется):

в) когда осуществляется ввод корректур (вероятность попадания от очереди к очереди изменяется):

где

п — общее количество выстрелов;

к — количество очередей;

S1, S2, Si — количество выстрелов в очереди;

Р1, Р2, Рк — вероятность попадания при одном выстреле первой, второй и т. д. очереди.

Пример. Определить вероятность поражения пулемета из автомата Калашникова (АКМ) одной очередью в 3 выстрела при стрельбе стоя из окопа на расстояние 300 м; ошибок в подготовке стрельбы нет (средняя траектория пройдет через середину цели).

Решение. 1, По таблицам находим: Вв|= 0,12 м, Вб1 — 0,11 м, Вв сумпос — 0,23 м, Вб сумпос= 0,33 м; из приложения 4 (табл. 6) приведенные размеры цели равны: высота 0,48 м, ширина 0,65 м.

2. Определяем вероятность попадания для первой пули очереди

3. Определяем вероятность попадания для последующей пули очереди:

4. Определяем вероятность поражения цели очередью в 3 выстрела:

Если вероятность попадания от выстрела к выстрелу не изменяется, вероятность поражения цели может быть определена по таблице вероятностей поражения цели (приложение 4, табл. 4), рассчитанной для различной величины вероятности попадания (р) и числа выстрелов (п).

Пример. Определить вероятность поражения противотанкового гранатомета при стрельбе из ручного пулемета Калашникова одной очередью в 5 выстрелов, если вероятность попадания равна 0,30.

Решение. По табл. 4 приложения 4 в вертикальной графе, обозначенной буквой р находим значение вероятности попадания, равное 0,30; в горизонтальной строчке против числа, соответствующего числу выстрелов (n), равному 5, находим вероятность поражения цели; она равна p1=0,83, или 83%.

При определении вероятности поражения целей матическим огнем по формулам, указанным в ст. 119 и 120, получаются завышенные результаты (на 3 — 7%). Поэтому при более точных подсчетах вероятностей поражения цели пользуются специальными формулами, учитывающими коэффициент зависимости выстрелов.