Математическое ожидание числа (процента) пораженных фигур групповой цели

121. Математическим ожиданием числа (процента) пораженных фигур в групповой цели называется среднее число (процент) пораженных фигур, которое можно получить, если повторить стрельбу большое число раз в одинаковых условиях.

122. Среднее число пораженных фигур в групповой цели численно равно сумме вероятностей поражения всех одиночных фигур. Если групповая цель состоит из одинаковых по размерам фигур, то среднее число пораженных фигур в групповой цели (AN) численно равно вероятности поражения одной фигуры (Pi), умноженной на число фигур в ней (N), т. е.

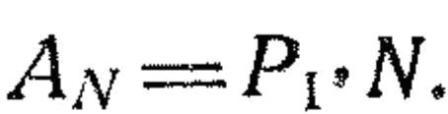
Если неизвестно количество фигур, составляющих групповую цель, то математическое ожидание числа пораженных фигур характеризуется средним ожидаемым процен­том пораженных фигур в ней.

Средний ожидаемый процент пораженных фигур в групповой цели, состоящей из одинаковых по размерам фигур, при стрельбе с искусственным рассеиванием или последовательным переносом огня численно равен вероятности поражения любой одиночной фигуры групповой цели при том же числе выстрелов, т. е.

An = Pi (в процентах).

Пример. Определить средний ожидаемый процент пораженных фигур в групповой дели, состоящей из грудных фигур, замаскированных в кустарнике на фронте 40 мна расстоянии 300 м, при стрельбе из станкового пулемета СГМВ 100 патронами с рассеиванием на ширину кустарника, если ошибок в стрельбе нет (средняя траектория по высоте пройдет посредине цели).

Решение. 1. По таблицам находим В<=0,15 м; при стрельбе с рассеиванием по фронту Вв увеличивается в 1,4 раза; из приложения 4 (табл. 6) высота цели равна 0,5 м, площадь одной фигуры 0,20 ,м2.

2. Определяем срединное отклонение по высоте при стрельбе с рассеиванием по фронту:

Вв = 0,15м • 1,4 = 0,21м

3. Определяем вероятность попадания в полосу, равную высоте цели:

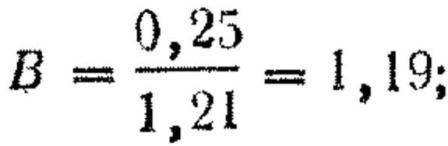
по табл. 1 приложения 4 находим

Рв = 0,578.

4. Определяем вероятность попадания в одну фигуру групповой цели:

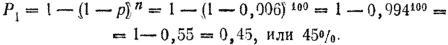
5. Определяем вероятность поражения одной фигуры групповой цели:

6. Средний ожидаемый процент пораженных фигур в групповой цели будет равен вероятности поражения одиночной фигуры этой цели, т.е. 45%.

Это означает, что при большом числе таких стрельб по 100 выстрелов при возможно одинаковых условиях можно на каждую стрельбу ожидать в среднем 45% пораженных фигур от общего их количества, однако при некоторых из этих стрельб процент пораженных фигур может быть больше или меньше среднего процента.